数据算法之二叉树一

算法和数据结构是程序的基本功，而且语言都是想通的，只要是掌握了一门语言学习其他语言就如同顺水推舟。

从今天开始要把这个系列写下去，虽然网上一搜一大堆，但是我写的这个系列，一方面是分享，一方面是让自己更深入的理解。

今天开始第一篇，二叉树。

什么是树？

树是计算机科学中经常用到的一种数据结构;
树是一种非线性的数据结构,以分层的方式存储数据;
树被用来存储具有层级关系的数据,比如文件系统中的文件;树还被用来存储有序列表;
查找、添加、删除元素性能要优于链表及数组;
树由一组以边连接的节点组成;

树的相关名词

父节点，子节点，兄弟节点：这个不用解释都知道吧
结点的度：就是分支数
树的度: 最大的结点度,最大也是2
叶子结点：没有子节点的结点
结点的层数：就是树有几层
左节点
右节点

一棵树最上面的节点称为根节点，如果一个节点下面连接多个节点，那么该节点称为父节点,它下面的节点称为子节点。一个节点可以有0个、1 个或多个子节点。没有任何子节点的节点称为叶子节点。二叉树每个节点的子节点不允许超过两个。

一个父节点的两个节点称为左节点和右节点。如下图的“B”为左节点，“C”为右节点。

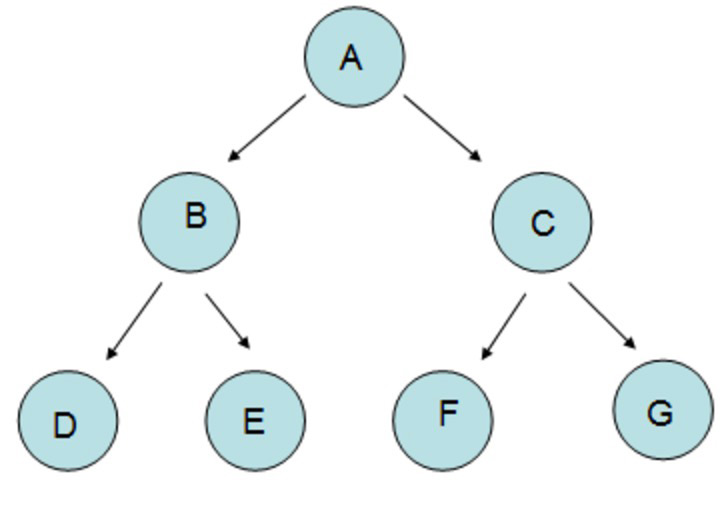
二叉树的性质　

JS实现二叉树

二叉树中每一个节点都是一个对象，每一个数据节点都有三个指针，分别是指向父母、左孩子和右孩子。定义一个节点对象Node，先定义左右两边的指针:

function Node(data, left, right) {
    this.data = data;      //用于存储数据
    this.left = left;      //左节点
    this.right = right;    //右节点
    this.show = show;      //显示保存在节点中的数据
}

function show() {
    return this.data;
}

新建一个类，用于表示二叉查找树BST

function BST() {
    this.root = null;       //用于表示根节点，并初始化为null
    this.insert = insert;   //插入节点的方法

    this.preOrder = preOrder; //先序遍历
    this.inOrder = inOrder; //中序遍历
    this.postOrder = postOrder; //后序遍历

    this.getMin = getMin;
    this.getMax = getMax;
    this.find = find;

    this.remove = remove;         //简单地接受待删除数据 
    this.removeNode = removeNode; //删除
}

大的框架已经写好了，现在开始插入节点

首先捋一遍思路：

先创建一个对象，将数据传入保存，检查BST是否有根节点，如果没有，就是棵新树，该节点就是根节点，结束；如果树中有根节点了，就要遍历整个树，给待插入节点找到插入的适当位置，这个时候就需要增加一个变量存储当前节点，一层层的遍历树，直到找到正确的位置时，跳出循环。

其实这时脑子还是一团浆糊，再细化一下：

判断有无根节点，没有的话，插入到根节点;
如果待插入节点保存的数据小于当前节点，则设新的当前节点为原节点的左节点; 反之，执行第 4 步;
如果当前节点的左节点为null，就将新的节点插入这个位置，退出循环; 反之，继续执行下一次循环;
设新的当前节点为原节点的右节点;
如果当前节点的右节点为null，就将新的节点插入这个位置，退出循环; 反之，继续执行下一次循环;

function insert(data) {
    var n = new Node(data, null, null),
        current,
 	parent;

    if (this.root == null) {
    	this.root = n;
    } else {
	current = this.root;   //根节点指向当前节点
	while(true) {
	    parent = current;  //根节点定义为父节点 
	    if (data < current.data) { 
		current = current.left;
		if (current == null) {
                    parent.left = n;
		    break; 
		}
	    } else {
		current = current.right;
		if (current == null) {
                    parent.right = n;
		    break; 
		}
	    }
	}
    }
}

现在 BST 类已经初步成型,但是操作上还只能插入节点，还需要有能力遍历BST，这样就可以按照不同的顺序,比如按照数字大小或字母先后,显示节点上的数据。

遍历的顺序

先序：根节点==>左子树==>右子树
中序：左子树==>根节点==>右子树
后序：左子树==>右子树==>根节点

中序遍历的代码：

function inOrder(node) {
    if (!(node == null)) {
       inOrder(node.left);
       console.log(node.show() + " ");
       inOrder(node.right);
    }
}

一个粟子：

var nums = new BST();
    nums.insert(23);
    nums.insert(45);
    nums.insert(16);
    nums.insert(37);
    nums.insert(3);
    nums.insert(99);
    nums.insert(22);
console.log(inOrder(nums.root));

结果是：

下图展示了中序的访问路径

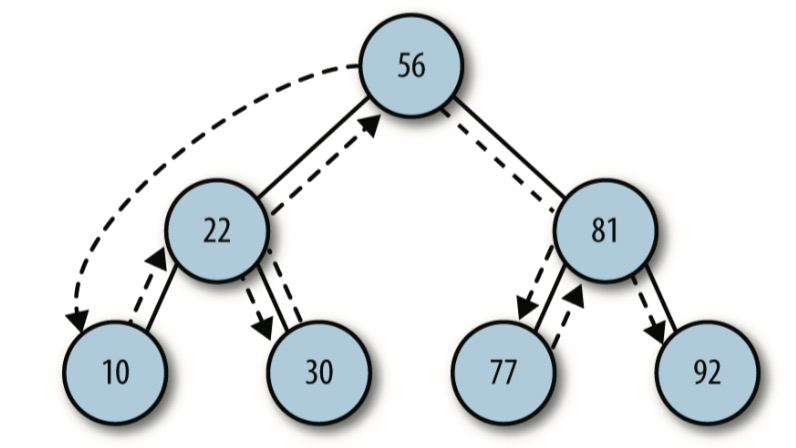
先序遍历的代码：

function preOrder(node) {
    if (!(node == null)) {
        console.log(node.show() + " ");
        preOrder(node.left);
        preOrder(node.right);
    } 
}

inOrder() 和 preOrder() 方法的唯一区别,就是 if 语句中代码的顺序。在 inOrder() 方法中,show() 函数像三明治一样夹在两个递归调用之间;在 preOrder() 方法中,show() 函数放在两个递归调用之前。

下图展示了先序的访问路径

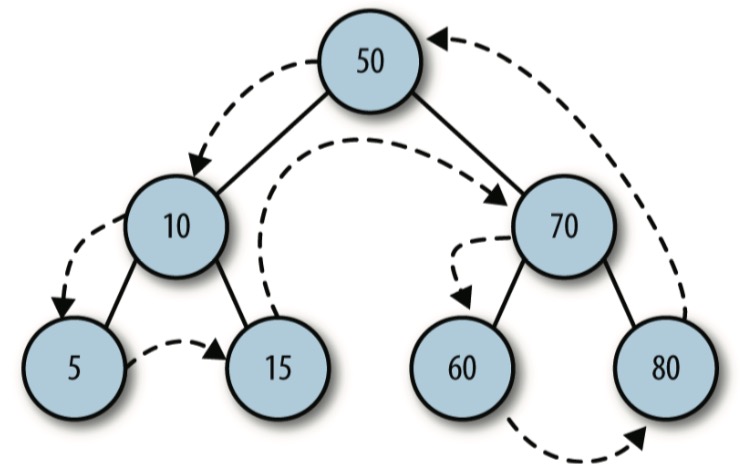
后序遍历postOrder() 方法的实现:

function postOrder(node) {
    if (!(node == null)) {
       postOrder(node.left);
       console.log(node.right);
       putstr(node.show() + " ");
    }
}

下图展示了后序的访问路径

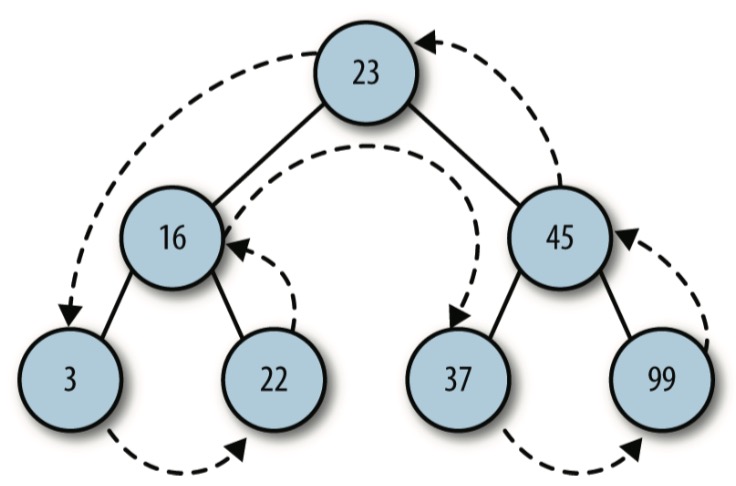
二叉树的查找

对 BST 通常有下列三种类型的查找:

查找给定值;
查找最小值;
查找最大值。

这三种查找中，最大值和最小值最简单，最大值都在右子树上，遍历右子树，找到最后一个节点即可，最小值同理。

最大值：

function getMax() {
   var current = this.root;
   while (!(current.right == null)) {
      current = current.right;
   }
   return current.data;
}

最小值：

function getMin() {
    var current = this.root;
    while (!(current.left == null)) {
        current = current.left;
    }
    return current.data;
}

上面两个程序直到遍历到最边上的节点，该节点为 current.left 或 current.right == null 时结束

来个例子：

var nums = new BST();
     nums.insert(23);
     nums.insert(45);
     nums.insert(16);
     nums.insert(37);
     nums.insert(3);
     nums.insert(99);
     nums.insert(22);

     var min = nums.getMin();
     print("minimum value: " + min);
     print("\n");
     var max = nums.getMax();
     print("maximum value: " + max);

结果：

再看看查找结定值怎么写

从根节点开始找，等于根结点就返回，不等的话，再从左子树开始找，找不到再从右子树开始找，直到子树中的值为 null 时结束。

function find(data) {
   var current = this.root;
   while (current != null) {
       if (current.data == data) {
          return current;
       }  else if (data < current.data) {
           current = current.left;
       } else {
           current = current.right;
       }
  }
   return null;
}