数据算法之二叉树二

从二叉查找树上删除节点

删除节点分几种情况：

删除的节点没有子节点
删除的节点只有左子树或只有右子树
删除的节点既有左子树又有右子树

思路：

从BST中删除节点,先是判断当前节点是否包含待删除的数据,
    1) 如果包含，则删除该节点;
    2) 如果不包含，则比较当前节点上的数据和待删除的数据。
        ① 如果待删除数据小于当前节点上的数据，则移至当前节点的左子节点继续比较;
        ② 如果删除数据大于当前节点上的数据，则移至当前节点的右子节点继续比较。

删除

如果待删除节点没有节点，那么只需要将从父节点指向它的链接指向null。
如果待删除节点只包含一个子节点，那么原本指向它的节点就得做些调整，使其指向它的子节点。
如果待删除节点包含两个子节点,正确的做法有两种:
1) 查找待删除节点左子树上的最大值
2) 查找待删除节点右子树上的最小值

移除一个叶节点

第一种情况是该节点没有子节点，要做的就是给这个节点赋予null值来移除它，但是每个节点除了自已包含的节点，还存在一个和父级的关系，所以这里仅赋一个null值是不够的，还需要处理指针。

如下图所示是一个删除叶节点的路径

如果想删除节点6，和当前的根节点进行比较，小于根节点就在左子树上找，反之在右子树上找，6比11小，所以接着左子树第一个节点7和6比较，又小于7接着与7节点的左子树5比较，6大于5接向5节点的右子树查找，最终找到6，这是一个查找的过程，然后再进行删除工作。

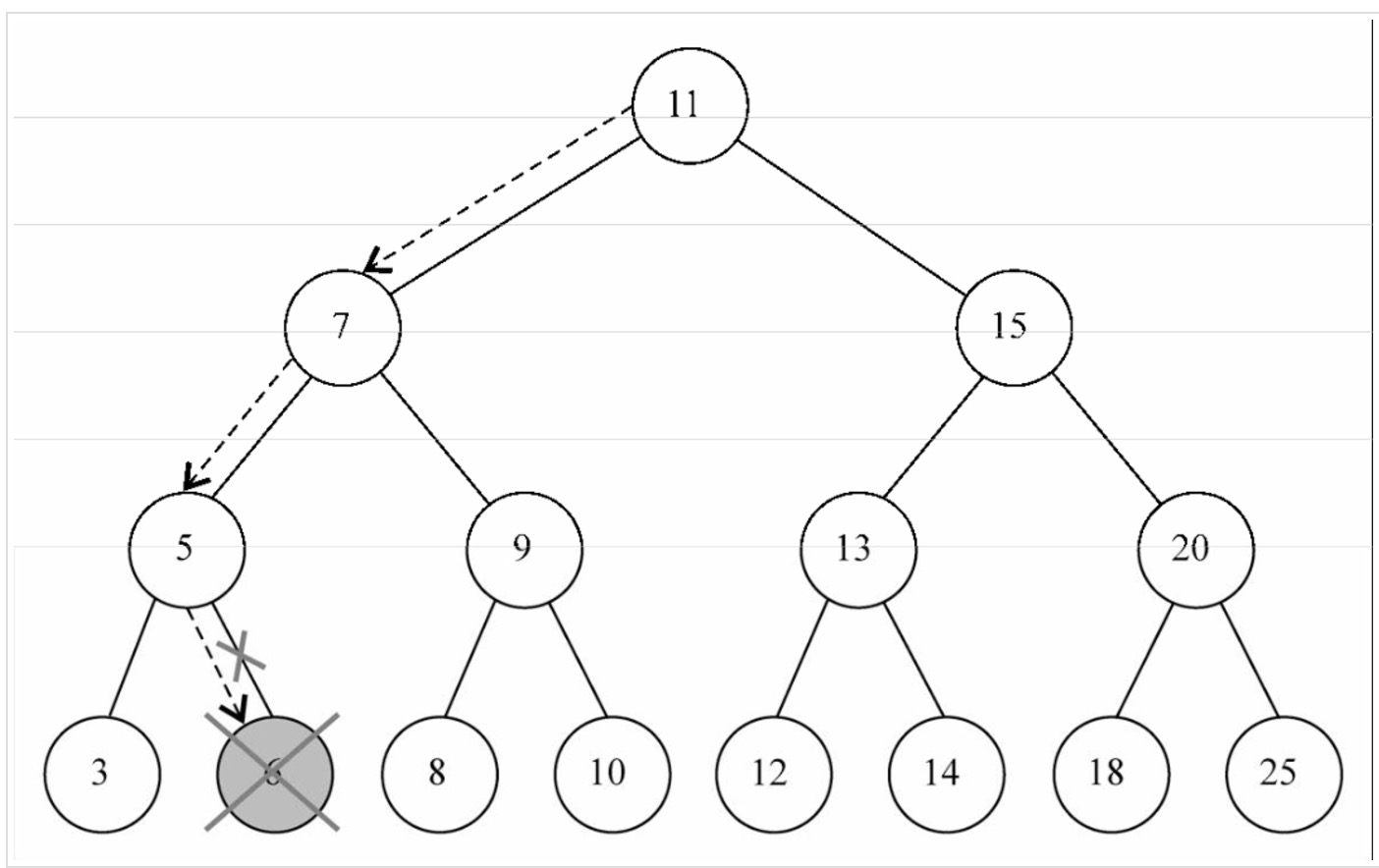
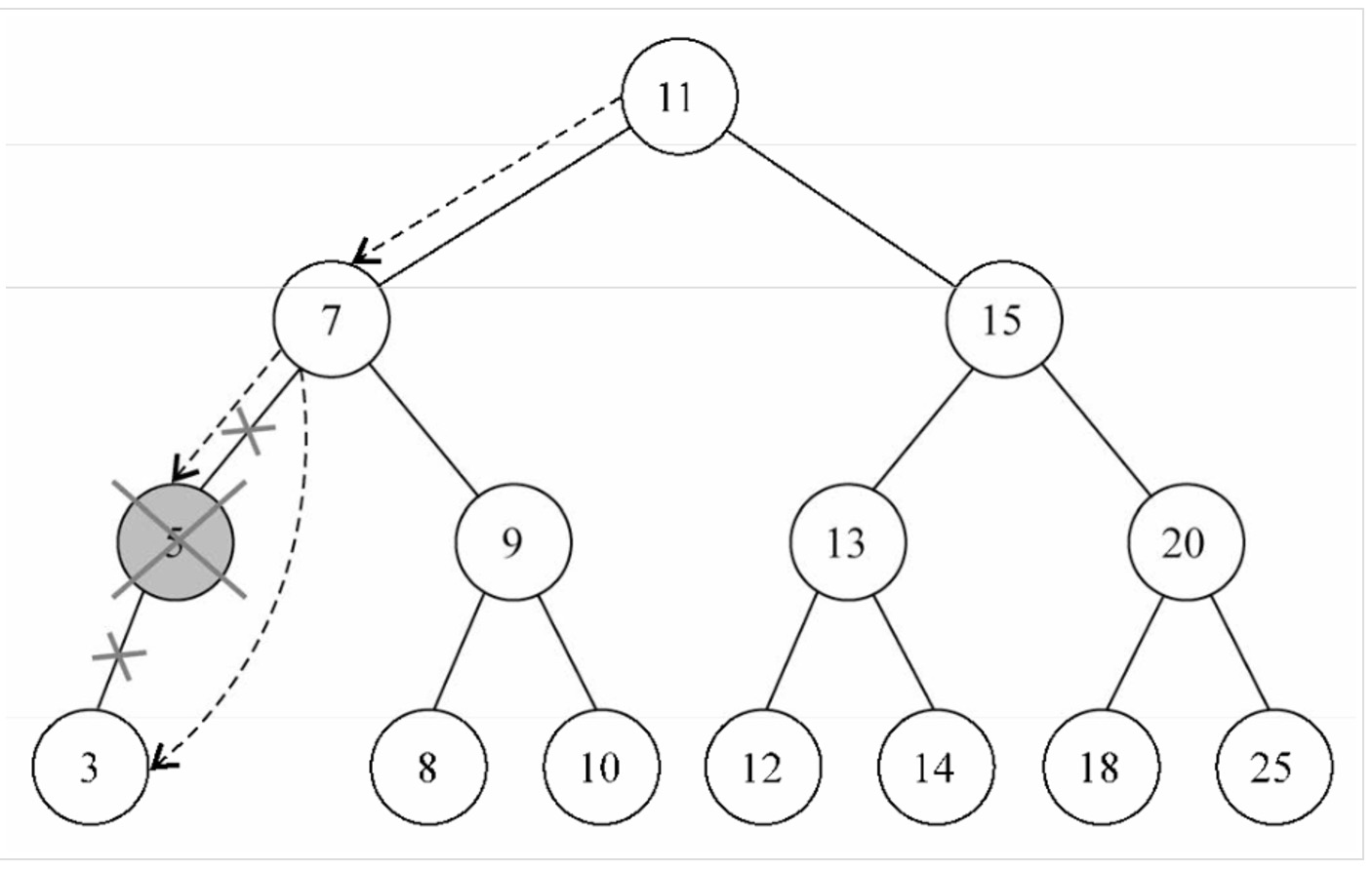
移除有一个左侧或右侧子节点的节点

移除有一个左侧子节点或右侧子节点的节点。这种情况下，需要跳过这个节点，直接将父节点指向它的指针指向子节点。

如果这个节点没有左侧子节点，也就是说它有一个右侧子节点。因此我们把对它的引用改为对它右侧子节点的引用并返回更新后的节点。

如果这个节点没有右侧子节点，也是一样——把对它的引用改为对它左侧子节点的引用并返回更新后的值。

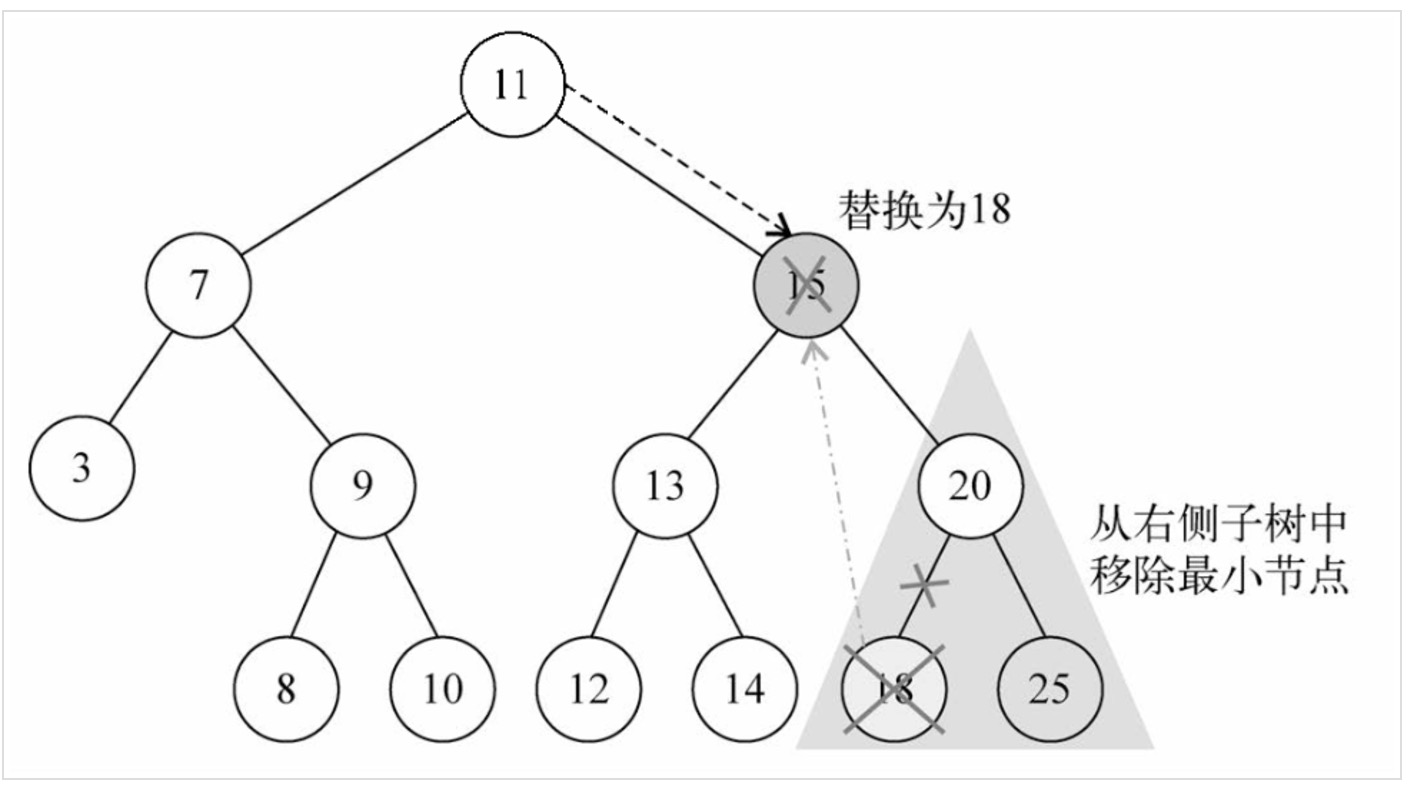
移除有两个子节点的节点

大概的分为下面三步：

查找的过程就不说了，找到这个要删除的点后，需要找到它右子树中的最小节点
这个小最节点替换要删除的节点，同时把右子树中的最小节点删除
后向它的父节点返回更新后的引用

理通了上面的思路后，就开始上代码了

定义两个方法：remove() 和 removerNode();

//用于简单地接受待删除数据
function remove(data) {
   root = removeNode(this.root, data);
}

//删除
function removeNode(node, data) {
  if (node == null) {
     return null;
  }

  if (data == node.data) {
    // 没有子节点的节点
    if (node.left == null && node.right == null) {
      return null;
    }
    // 没有左子节点的节点
    if (node.left == null) {
      return node.right;
    }
    // 没有右子节点的节点
    if (node.right == null) {
      return node.left;
    }
    // 有两个子节点的节点
    var tempNode = getSmallest(node.right);
    node.data = tempNode.data;
    node.right = removeNode(node.right, tempNode.data); return node;
  } else if (data < node.data) {
       node.left = removeNode(node.left, data);
       return node;
  } else {
       node.right = removeNode(node.right, data);
       return node;
  }
}