图和图算法(一)

这一章不好理解，所以分为两期来做。

如何用图给网络建模? 如何用 JavaScript 表示图? 如何实现重要的图算法?

带着这几个问题开始今天的学习

相关概念

• 图: 图由边的集合及顶点的集合组成
• 有向图: 如果一个图的顶点对是有序的，则可以称之为有向图，有向图表明了顶点的流向
• 无向图: 如果图是无序的，则称之为无序图，或无向图
• 路径: 图中的一系列顶点构成路径,
• 路径的长度: 用路径中第一个顶点到最后一个顶点之间边的数量表示
• 环: 由指向自身的顶点组成的路径称, 环的长度为0
• 圈: 是至少有一条边的路径，且路径的第一个顶点和最后一个顶点相同
• 简单圈: 无论是有向图还是 无向图，只要是没有重复边或重复顶点的圈
• 平凡圈: 除了第一个和最后一个顶点以外，路径的其他顶点有重复的圈
• 如果两个顶点之间有路径，那么这两个顶点就是强连通的，反之亦然。如果有向图的所有 的顶点都是强连通的，那么这个有向图也是强连通的

有向图

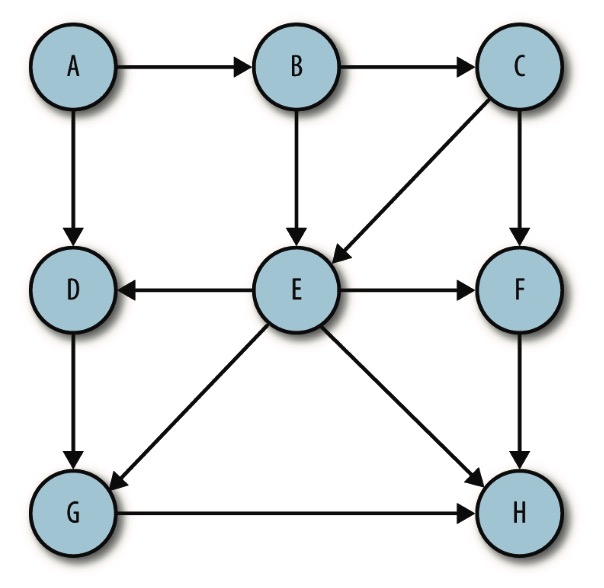
无向图

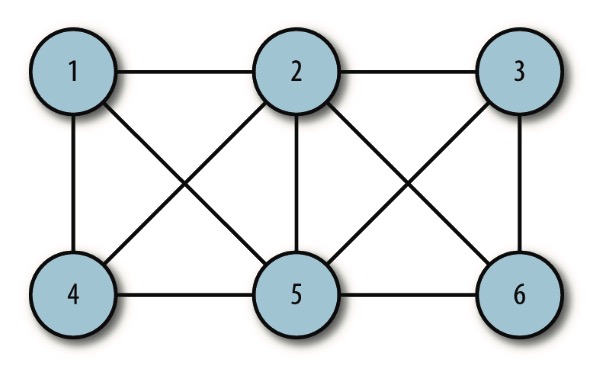
表示顶点

创建图类的第一步就是要创建一个 Vertex 类来保存顶点和边。这个类的作用与链表和二叉搜索树的 Node 类一样。

Vertex 类有两个数据成员:

• 用于标识顶点，被命名为 label
• 表明这个顶点是否被访问过的布尔值, 被命名为wasVisited

function Vertex(label) {
    this.label = label;
}

表示边

图的实际信息都保存在边上面，因为它们描述了图的结构

表示边两种方法实现：

• 将表示图的边的方法称为邻接表或者邻接表数组，这种方法将边存储为由顶点的相邻顶点列表构成的数组，并以此顶点作为索引。使用这种方案，当在程序中引用一个顶点时，可以高效地访问与这个顶点相连的所有顶点的列表, 本节将选用这种表示方法。

邻接表

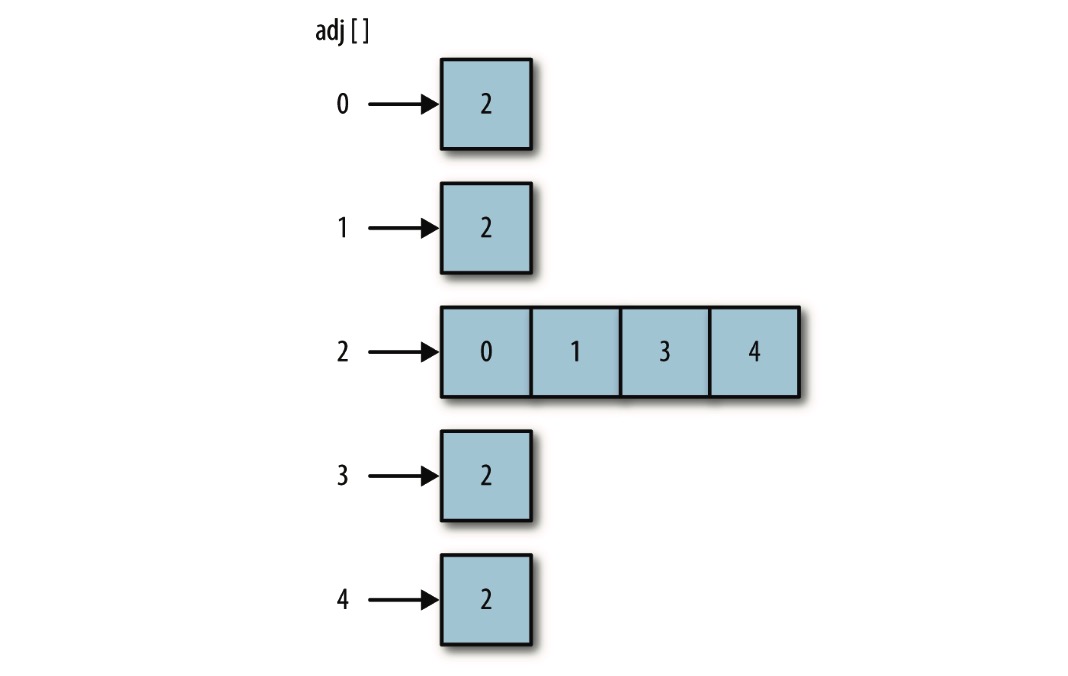
看上图，如果顶点 2 与顶点 0、1、3、4 相连，并且它存储在数组中索引为 2 的位置，那么，访问这个元素，我们可以访问到索引为 2 的位置处由顶点 0、1、3、4 组成的数组

• 另一种表示图边的方法被称为邻接矩阵。它是一个二维数组，其中的元素表示两个顶点之间是否有一条边

构建图

确定了如何在代码中表示图之后，构建一个表示图的类就很容易了。下面是第一个Graph类的定义

function Graph(v) {
    this.vertices = v;
    this.edges = 0;
    this.adj = [];
    for (var i = 0; i < this.vertices; ++i) {
       this.adj[i] = [];
       this.adj[i].push("");
    }
    this.addEdge = addEdge;
    this.showGraph = showGraph;
}

这个类会记录一个图表示了多少条边，并使用一个长度与图的顶点数相同的数组来记录顶点的数量。通过 for 循环为数组中的每个元素添加一个子数组来存储所有的相邻顶点，并 将所有元素初始化为空字符串。

• addEdge() 函数

function addEdge(v, w) {
    this.adj[v].push(w);
    this.adj[w].push(v);
    this.edges++;
}

当调用这个函数并传入顶点 A 和 B 时，函数会先查找顶点 A 的邻接表，将顶点 B 添加到列 表中，然后再查找顶点 B 的邻接表，将顶点 A 加入列表。最后，这个函数会将边数加 1。

• showGraph() 函数

showGraph() 函数会通过打印所有顶点及其相邻顶点列表的方式来显示图:

function showGraph() {
    for (var i = 0; i < this.vertices; ++i) {
       document.write(i + "->");
       for (var j = 0; j < this.vertices; ++j) {
           if (this.adj[i][j] != undefined) {
               document.write(this.adj[i][j] + ' ');
           }
       }
    }
}

初始化一个例子：

g = new Graph(5);
g.addEdge(0,1);
g.addEdge(0,2);
g.addEdge(1,3);
g.addEdge(2,4);
g.showGraph();

输出结果：

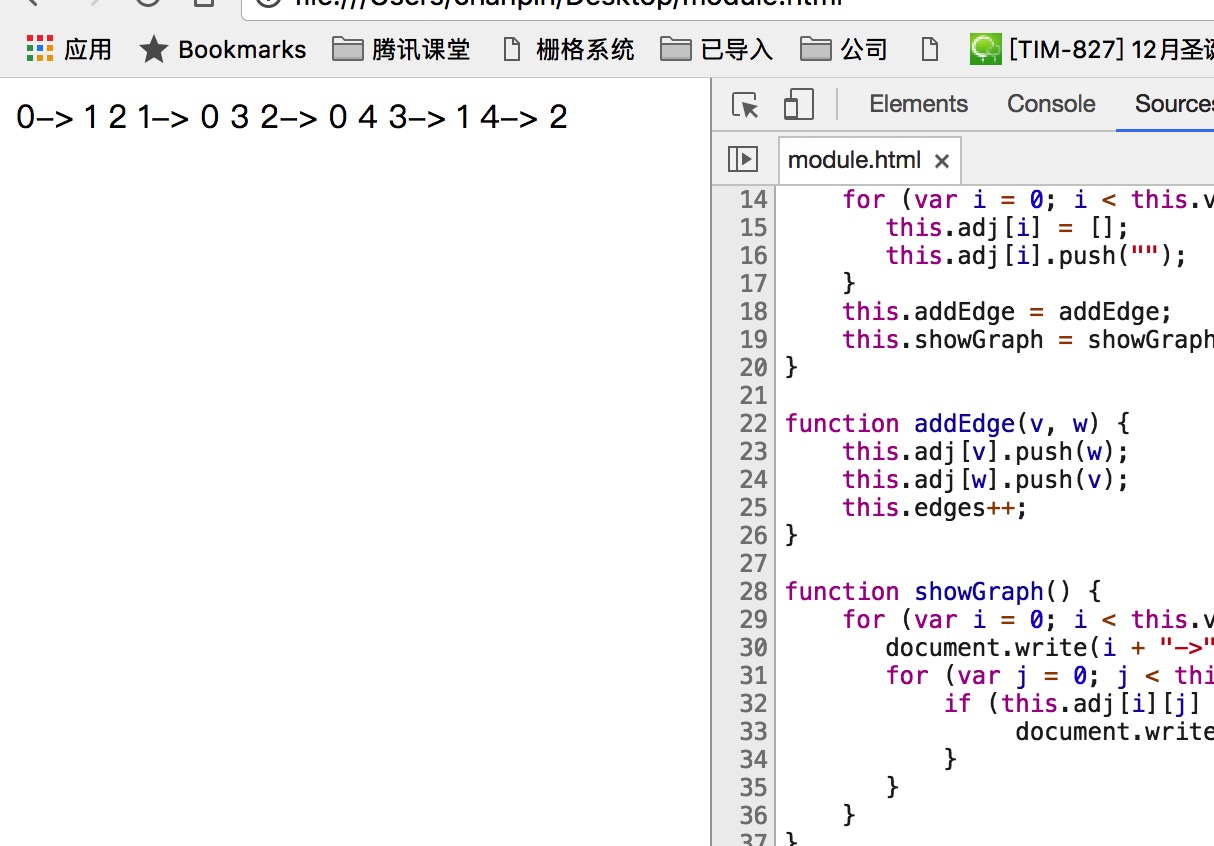
还是这样看更直观些：

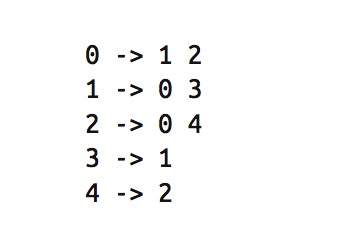
• 顶点 0 有到顶点 1 和顶点 2 的边;
• 顶点 1 有到顶点 0 和顶点 3 的边;
• 顶 点2有到顶点0和4的边;
• 顶点3有到顶点1的边;
• 顶点4有到顶点2的边。

当然，这种显示存在冗余，例如，顶点 0 和 1 之间的边和顶点 1 到 0 之间的边相同。如果只是为了显示，这样是不错的，但是在开始探索图的路径之前，需要调整一下输出。

搜索图及对图的操作

• 确定从一个指定的顶点可以到达其他哪些顶点，这是经常对图执行的操作。

可能想通过地图了解到从一个城镇到另一个城镇有哪些路，或者从一个机场到其他机场有哪些航班。 图上的这些操作是用搜索算法执行的。

• 在图上可以执行两种基础搜索: 深度优先搜索和广度优先搜索。

深度优先搜索

深度优先搜索包括从一条路径的起始顶点开始追溯，直到到达最后一个顶点，然后回溯， 继续追溯下一条路径，直到到达最后的顶点，如此往复，直到没有路径为止。这不是在搜 索特定的路径，而是通过搜索来查看在图中有哪些路径可以选择。

如下图演示了深度优先

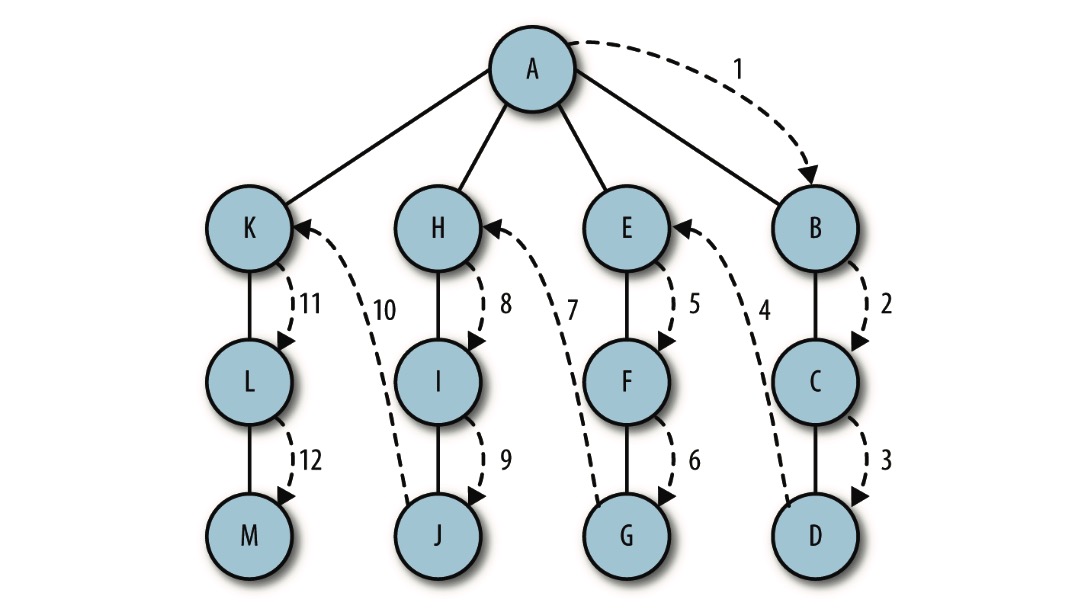
深度优先搜索算法比较简单:访问一个没有访问过的顶点，将它标记为已访问，再递归地去访问在初始顶点的邻接表中其他没有访问过的顶点。

要让该算法运行，需要为 Graph 类添加一个数组，用来存储已访问过的顶点，将它所有元 素的值全部初始化为 false。

function Graph(v) {
    this.vertices = v;
    this.edges = 0;
    this.adj = [];
    for (var i = 0; i < this.vertices; ++i) {
       this.adj[i] = [];
       this.adj[i].push("");
    }
    this.addEdge = addEdge;
    this.showGraph = showGraph;
    this.dfs = dfs;

    this.marked = [];
    for (var i = 0; i < this.vertices; ++i) {
       this.marked[i] = false;
    }
}

深度优先搜索函数

function dfs(v) {
    this.marked[v] = true;
    document.write("Visited vertex:  " + v);
    for each(var w in this.adj[v]) {
       if (!this.marked[w]) {
          this.dfs(w);
       } 
    }
}

广度优先搜索

广度优先搜索从第一个顶点开始，尝试访问尽可能靠近它的顶点。本质上，这种搜索在图 上是逐层移动的，首先检查最靠近第一个顶点的层，再逐渐向下移动到离起始顶点最远的 层。

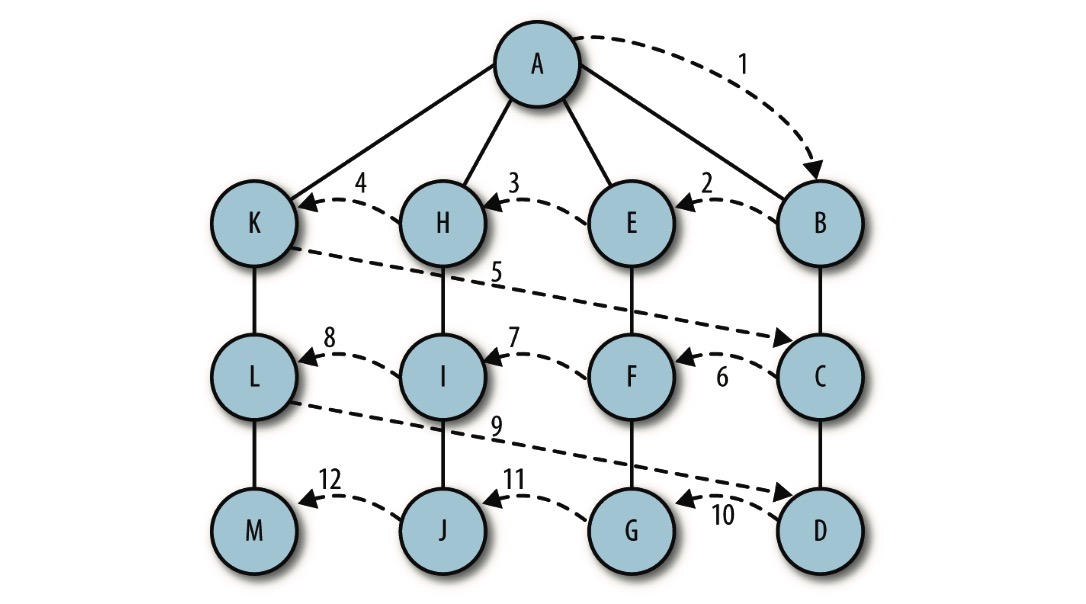
广度优先搜索算法使用了抽象的队列而不是数组来对已访问过的顶点进行排序。其算法的 工作原理如下:

• 查找与当前顶点相邻的未访问顶点，将其添加到已访问顶点列表及队列中;
• 从图中取出下一个顶点 v，添加到已访问的顶点列表;
• 将所有与 v 相邻的未访问顶点添加到队列。

function bfs(s) {
    var queue = []; 
    this.marked[s] = true; 
    queue.push(s); //添加到队尾
    while (queue.length > 0) {
	var v = queue.shift(); //从队首移除 
	   if (v == undefined) {
              document.write("Visisted vertex:  " + v);
           }
           for each(var w in this.adj[v]) {
              if (!this.marked[w]) {
                 this.edgeTo[w] = v;
                 this.marked[w] = true;
                 queue.push(w);
	      } 
	   }
    } 
}